W świecie finansów i matematyki, precyzyjne przeliczenia stają się nieodzowne. W takich przypadkach Excel staje się naszym niezastąpionym sojusznikiem, a jedną z funkcji, która pomaga w dokładnych obliczeniach, jest NOMINALNA(). Jest to funkcja umożliwiająca przeliczanie wartości efektywnych stóp procentowych na stopy nominalne.
Nominalna roczna stopa procentowa: To pierwotna, wyrażona w procentach wartość stopy procentowej, która nie uwzględnia kapitalizacji, czyli procesu zwiększania wartości początkowej inwestycji poprzez narastający wzrost zysków i odsetek w kolejnych okresach. Nominalna- jest to pojęcie oznaczające podstawową wartość, nie uwzględniającą żadnych modyfikacji lub efektów dodatkowych.
Efektywna roczna stopa procentowa: To roczna stopa procentowa, która uwzględnia częstotliwość kapitalizacji odsetek. Jest to rzeczywista stopa, którą otrzymasz lub zapłacisz w wyniku kapitalizacji. Wskaźnik ten służy określeniu wzrostu wartości kapitału w skali roku.
Do czego służy funkcja NOMINALNA() ?
Funkcja NOMINALNA() znajduje zastosowanie w dziedzinach takich jak finanse, ekonomia, rachunkowość oraz wszędzie tam, gdzie dokładne przeliczenia efektywnych stóp procentowych są istotne. Banki, instytucje finansowe, analitycy finansowi, planiści budżetowi, osoby zarządzające inwestycjami oraz wszyscy ci, którzy zajmują się oceną opłacalności różnych produktów finansowych, korzystają z funkcji NOMINALNA(), aby uzyskać dokładne dane na temat stóp procentowych i kosztów.
W praktyce funkcja ta pomaga w podejmowaniu mądrych decyzji finansowych, umożliwiając dokładne porównanie różnych opcji inwestycyjnych, kredytów lub lokat. Dzięki niej możliwe jest uniknięcie nieporozumień związanych z różnymi rodzajami kapitalizacji odsetek (ich narastaniem) i oszacowanie rzeczywistych kosztów lub zysków w dłuższej perspektywie czasowej.
Składnia funkcji NOMINALNA() jest niezwykle prosta:
NOMINALNA(stopa_efektywna; okresy)
stopa_efektywna: To jest argument wymagany, reprezentujący efektywną stopę procentową.
okresy: To również argument wymagany, oznaczający liczbę kapitalizacji w roku , czyli ile razy w ciągu jednego roku odsetki będą naliczane i dodawane do początkowej kwoty inwestycji lub pożyczki. Ten parametr pomaga określić, jak często odsetki zostaną skapitalizowane, co wpływa na całkowity zysk lub koszty w danym okresie. Na przykład, jeśli okresy wynoszą 4, oznacza to, że odsetki będą kapitalizowane kwartalnie, a jeśli wynoszą 12, to kapitalizacja odbywa się co miesiąc.
Warto zaznaczyć, że wartość argumentu okresy zostaje zaokrąglona do najbliższej liczby całkowitej. W przypadku, gdy którykolwiek z argumentów nie jest liczbą, funkcja zwróci błąd #ARG!.
Skąd mamy wiedzieć jaka jest wartość do pierwszego argumentu? Jak wyliczyć efektywną stopę procentową? Nic prostszego. Za pomocą funkcji EFEKTYWNA(), która ma na naszym blogu bardzo obszerne wyjaśnienie wraz z pojęciami finansowymi, które są niezbędne do zrozumienia tych funkcji – Funkcja EFEKTYWNA.
Jak przeliczyć stopę efektywną na nominalną?
Załóżmy, że mamy efektywną stopę procentową wynoszącą 6% i chcemy poznać odpowiadającą jej stopę nominalną przy skapitalizowaniu co kwartał. Wartości mogą być umieszczone w komórkach B3 i B6 odpowiednio.
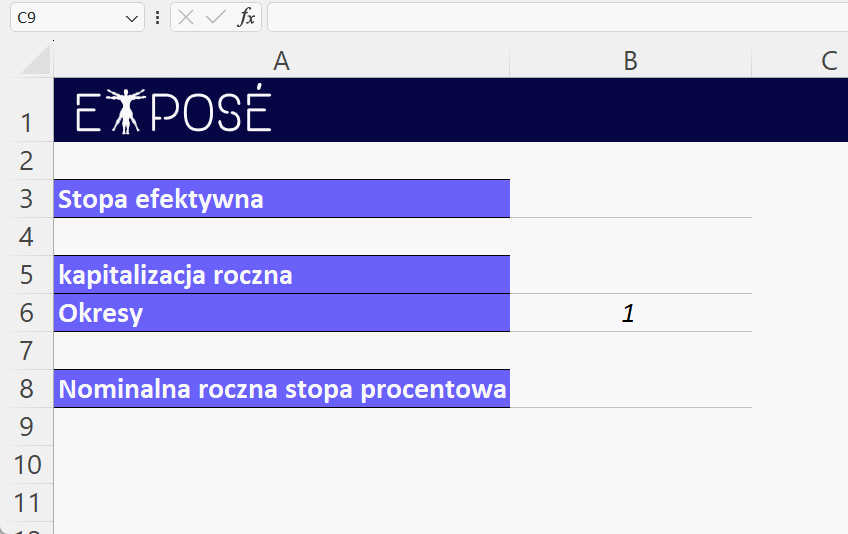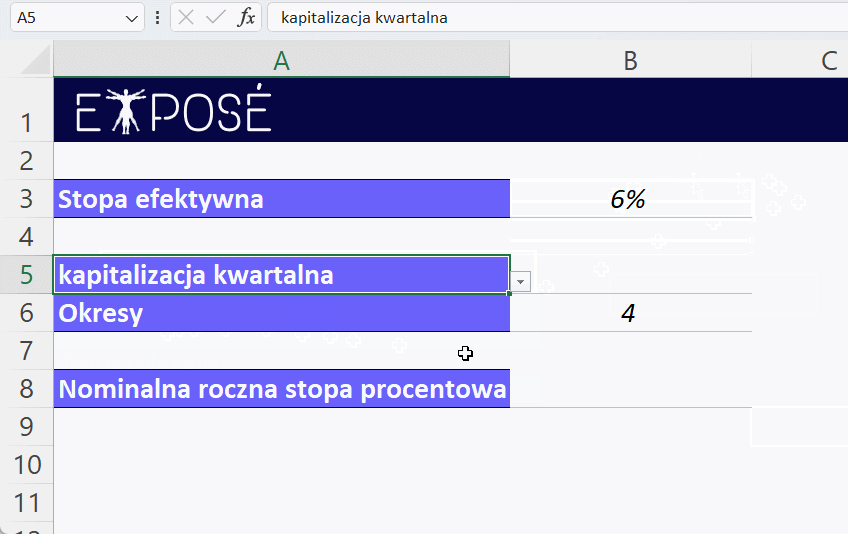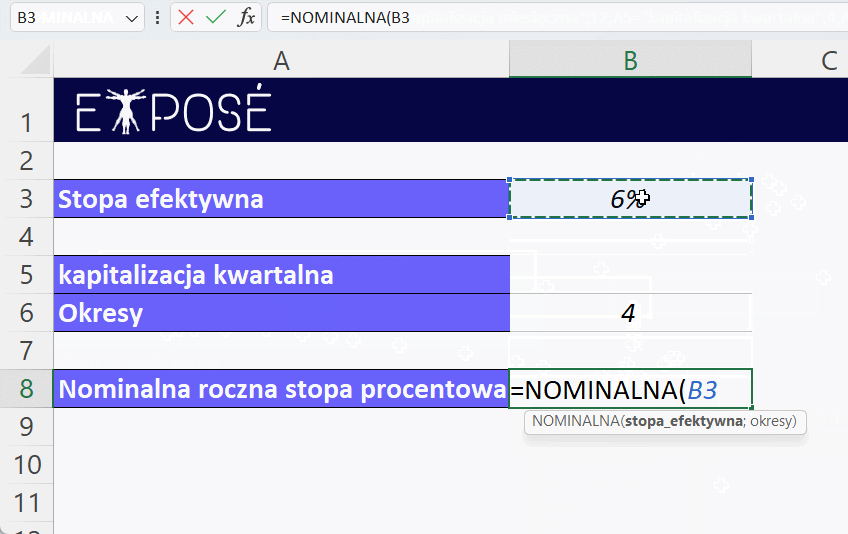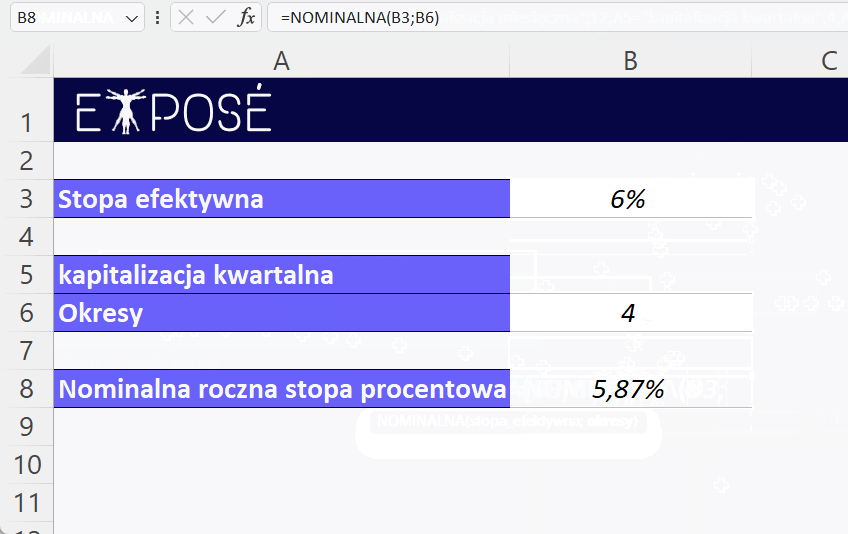
Funkcję, którą możemy wprowadzić w komórce B5, aby uzyskać wynik, to:
=NOMINALNA(B3; B6)
Otrzymamy wartość 0,0586953846746372, co w procentach daje nam około 5.87%.
Jak obliczyć półroczną stopę efektywną na nominalną?
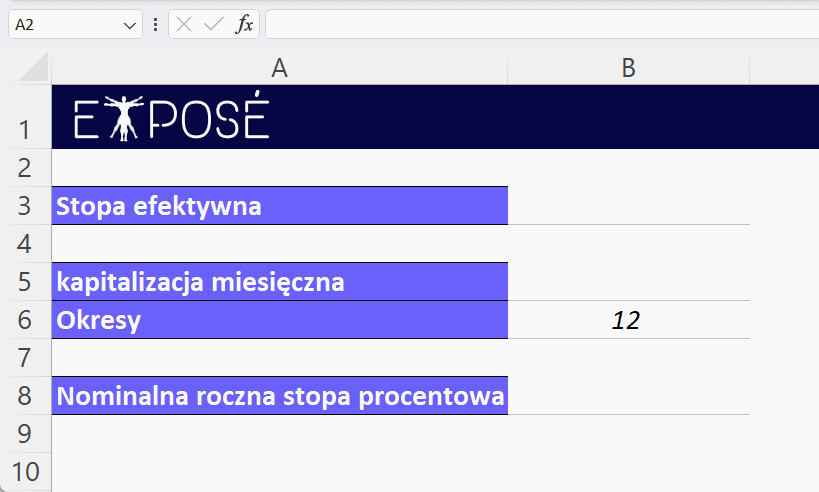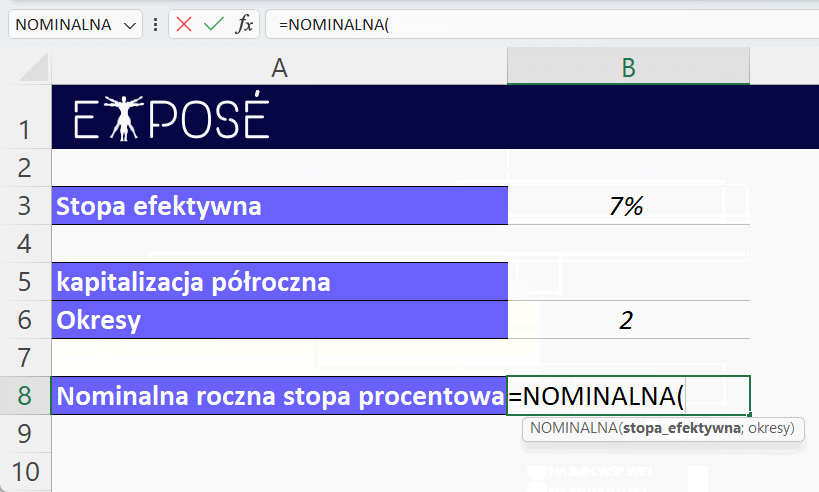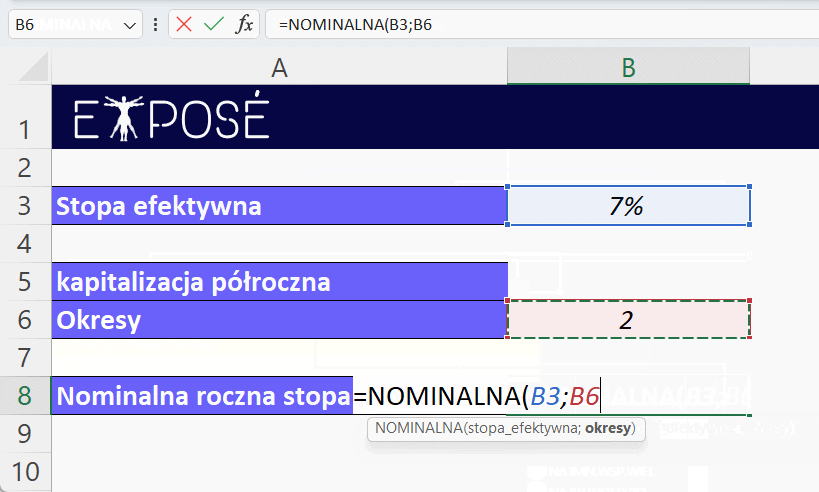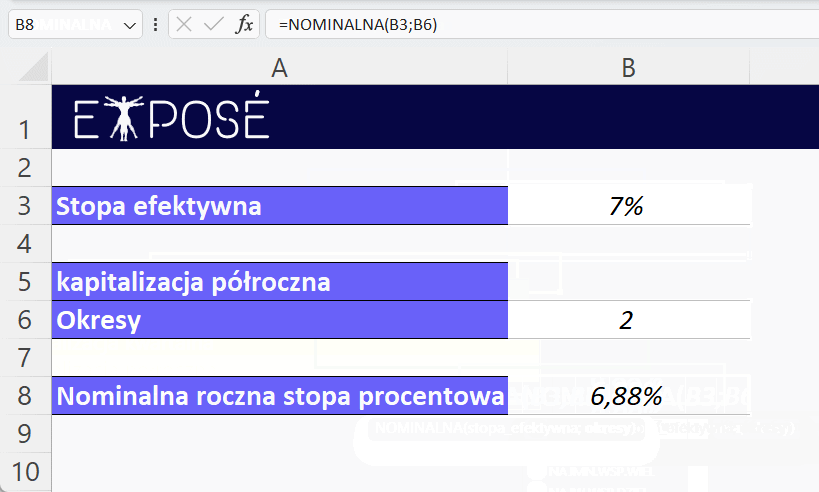
W przypadku, gdy mamy bardziej złożoną sytuację, gdzie efektywna stopa procentowa wynosi 7%, a skapitalizowana jest co pół roku, możemy wykorzystać funkcję NOMINALNA() tak samo jak wcześniej.
Funkcja w komórce B8 będzie wyglądać podobnie:
=NOMINALNA(B3; B6)
Wynik wynosi 0,0688160865577201, czyli około 6.88%.
W powyższych dwóch przykładach widzicie, że funkcja jest bardzo prosta w użyciu. W identyczny sposób możemy wykorzystać ją w praktyce np. w:
Kredyty i pożyczki
Funkcja NOMINALNA() znajduje także zastosowanie w dziedzinie kredytów i pożyczek. Wyobraźmy sobie, że mamy zaciągnąć kredyt o efektywnej stopie procentowej wynoszącej 12%, a bank dokonuje kapitalizacji odsetek co miesiąc. Aby zrozumieć, jakie będą nasze roczne koszty, musimy poznać stopę nominalną.
Finanse osobiste
Przykładem może być sytuacja, w której chcemy porównać oferty dwóch różnych instytucji finansowych. Pierwsza oferuje efektywną stopę procentową wynoszącą 5% i kapitalizuje odsetki kwartalnie, a druga oferuje 5.2% i kapitalizuje odsetki miesięcznie. Chcemy dowiedzieć się, która oferta jest korzystniejsza w perspektywie rocznej.
W kontekście ofert finansowych:
Dla inwestycji: Im wyższa stopa nominalna, tym większy będzie potencjalny zysk z inwestycji w skali roku.
Dla kredytów lub pożyczek: Im wyższa stopa nominalna, tym większe będą koszty związane z kredytem lub pożyczką w skali roku.
Funkcja NOMINALNA() to niezastąpione narzędzie, które umożliwia skuteczne przeliczanie efektywnych stóp procentowych na stopy nominalne. Jej prosta składnia i zastosowanie w rzeczywistych sytuacjach finansowych sprawiają, że jest to narzędzie, dzięki któremu możemy ustrzec się np. nieuczciwym praktykom parabanków lub innych pożyczkodawców.
Unikalna relacja między funkcjami NOMINALNA() a EFEKTYWNA() dodaje kolejny wymiar do możliwości, jakie oferuje Excel.
