W świecie finansów i analizy danych, precyzja i szybkość obliczeń odgrywają kluczową rolę w podejmowaniu trafnych decyzji. Microsoft Excel, jako narzędzie w tych dziedzinach, oferuje szereg zaawansowanych funkcji do analizy finansowej. Jedną z tych funkcji jest XNPV. XNPV to akronim od angielskiego terminu Extended Net Present Value, co można tłumaczyć jako Zdyskontowana Wartość Netto Przepływów Gotówkowych. Funkcja ta umożliwia obliczenie netto obecnej wartości przepływów gotówkowych, uwzględniając okresy nieregularnych płatności oraz różne stopy dyskontowe. Ta nieregularność jest tu kluczowa, ponieważ to ona odróżnia XNPV od NPV, o której obszernie piszemy na naszym blogu tutaj.
Różnice Między XNPV a NPV
Podczas gdy NPV (Net Present Value) to standardowa funkcja, która oblicza netto obecną wartość przepływów gotówkowych przy jednej stałej stopie dyskontowej, XNPV pozwala na uwzględnienie nieregularnych przepływów oraz różnych stóp dyskontowych. Dzięki temu, funkcja XNPV jest bardziej elastyczna i dokładniejsza w przypadkach, gdy przepływy gotówkowe są niestandardowe. To właśnie zdolność XNPV do operowania na nieregularnych danych, czyni ją bardziej rozbudowaną i użyteczną w bardziej skomplikowanych scenariuszach analizy finansowej.
Podobieństwa i Powiązania między XNPV a XIRR
XNPV oraz XIRR to dwie różne funkcje w programie Microsoft Excel, które są często używane w analizie finansowej. Oba te narzędzia służą do oceny inwestycji i przepływów gotówkowych, ale różnią się w pewnych aspektach. O XIRR więcej znajdziecie na naszym blogu tutaj.
XNPV pozwala na obliczenie netto obecnej wartości przepływów gotówkowych, uwzględniając daty tych przepływów oraz zadaną stopę dyskontową. Jest to szczególnie przydatne w przypadku przepływów nieregularnych.
XIRR z kolei jest funkcją, która pozwala obliczyć wewnętrzną stopę zwrotu (IRR) dla przepływów gotówkowych. IRR to stopa procentowa, przy której wartość netto przepływów gotówkowych jest równa zeru. Funkcja XIRR jest bardziej wszechstronna, ponieważ uwzględnia czas wartości pieniądza oraz nieregularne przepływy gotówkowe.
Po takim wstępie najwyższy czas przejść do naszej funkcji właściwej.
Składnia funkcji XNPV składa się z trzech głównych argumentów:
XNPV(stopa;wartości;daty)
Warto zauważyć, że w przypadku pierwszej płatności, funkcja XNPV pozwala na opcjonalne uwzględnienie kosztu lub płatności występującej na początku inwestycji. Wartość ta musi być ujemna, jeśli jest to koszt lub płatność.
Jak obliczyć obecną wartość netto przepływów gotówkowych?
Wyobraźmy sobie, że mamy następujące przepływy gotówkowe w różnych okresach i chcemy obliczyć ich netto obecną wartość przy założonej stopie dyskontowej:
| Wartości | Daty |
| -10000 zł | 2008-01-01 |
| 2750 zł | 2008-03-01 |
| 4250 zł | 2008-10-30 |
| 3250 zł | 2009-02-15 |
| 2750 zł | 2009-04-01 |
W komórkach arkusza Excel (począwszy od A4) wprowadzamy te dane. Następnie, w komórce D4, możemy użyć funkcji XNPV:
=XNPV(9%;A4:A8; B4:B8)
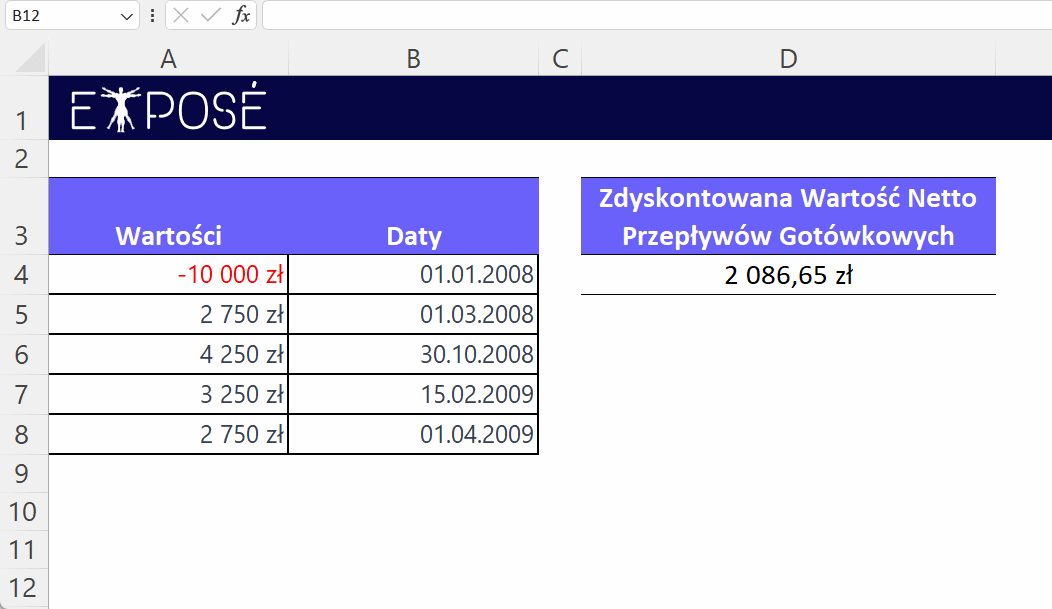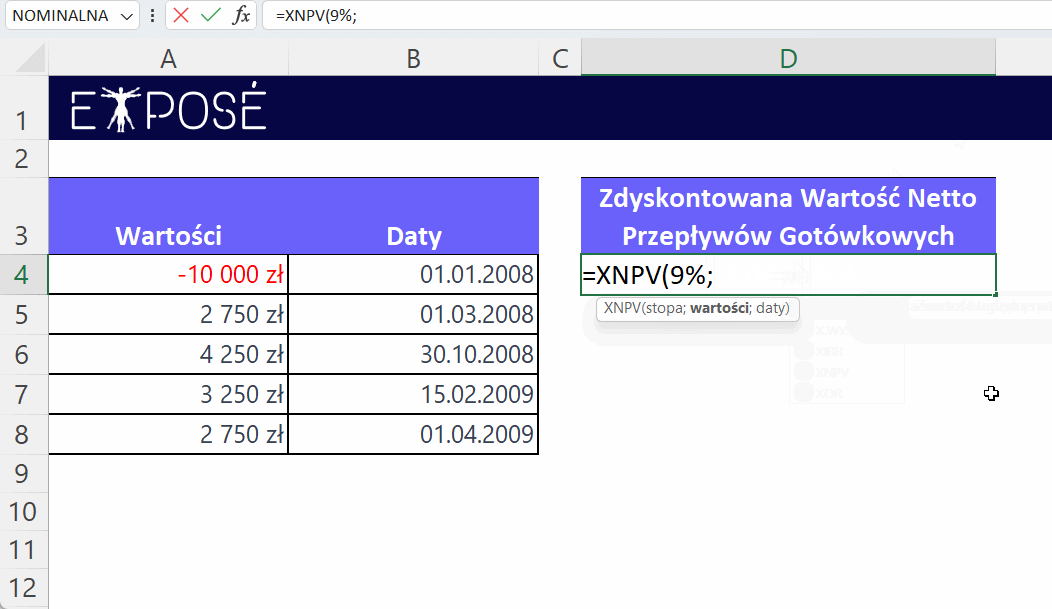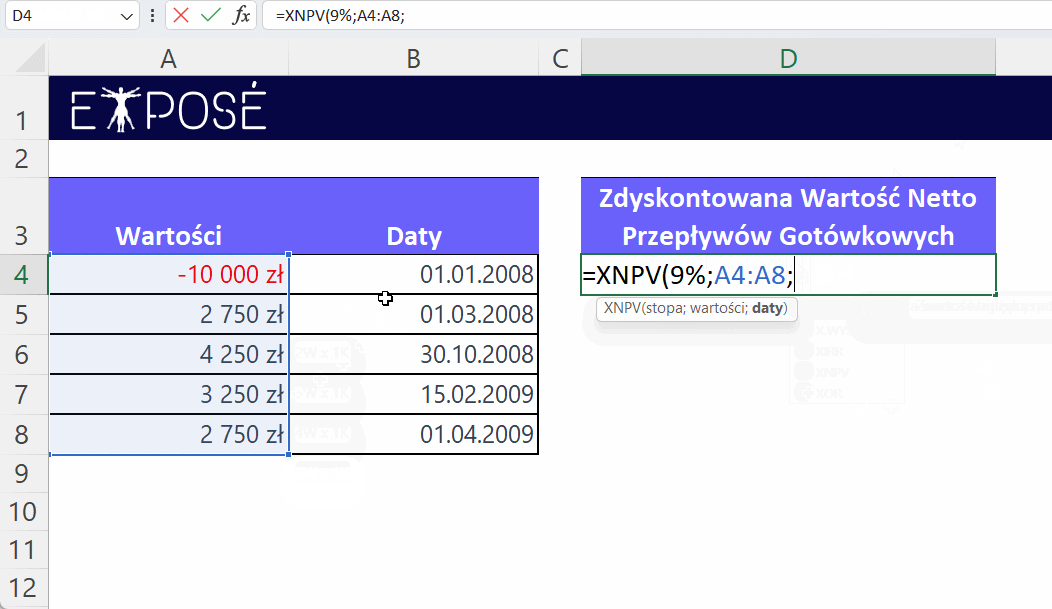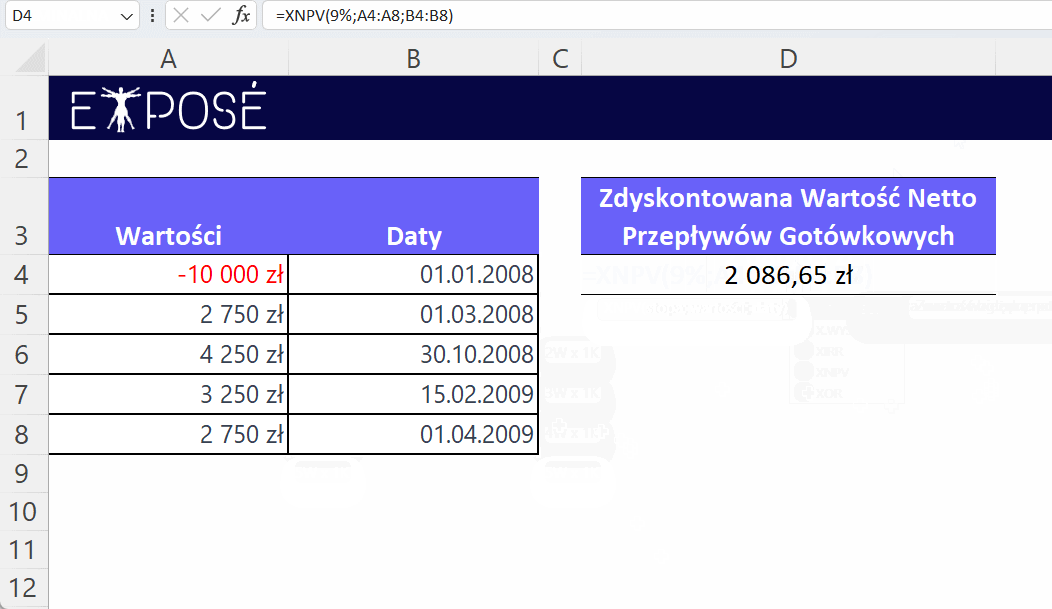
Wynik takiej formuły wynosi 2086,65 zł, co jest obecną wartością netto przepływów gotówkowych dla inwestycji przy 9% stopie dyskontowej. Ta kwota oznacza, ile dzisiejsza wartość przepływów pieniężnych, które się wydarzą w przyszłości, wynosi w rzeczywistości na dzisiejszą datę, uwzględniając pewną stopę procentową (9%).
Innymi słowy, jeśli mamy pewne pieniądze, które mają być wypłacone w przyszłości (na przykład w różnych terminach), wartość tych pieniędzy jest teraz 2086,65 złotych, jeśli wzięte są pod uwagę dwie rzeczy: (1) fakt, że wartość pieniądza zmniejsza się w czasie (czyli te przyszłe pieniądze mają mniejszą wartość dzisiaj) i (2) wymagana stopa zwrotu, która wynosi 9%. To oznacza, że aby inwestycja była opłacalna, musiałaby generować przynajmniej 9% zwrotu.
W skrócie, ten wynik pomaga nam zrozumieć, ile dzisiejsza wartość przyszłych przepływów pieniężnych wynosi, biorąc pod uwagę stopę procentową i fakt, że pieniądze w przyszłości są mniej warte niż dzisiaj. Kiedy używasz funkcji XNPV, chcesz dowiedzieć się, ile te przyszłe pieniądze są warte obecnie, w dniu, w którym przeprowadzasz analizę. To jest ważne, ponieważ wartość pieniądza zmienia się w czasie ze względu na inflację, zmiany stopy procentowej itp. Dlatego obliczenie dzisiejszej wartości jest istotne, aby dokładnie ocenić opłacalność przyszłych przepływów gotówkowych.
Należy zwrócić uwagę, że dane w naszym fikcyjnym przykładzie mają również stare fikcyjne daty. W rzeczywistości ważne jest, aby upewnić się, że są one nadal aktualne i istotne w kontekście obecnej sytuacji. Jeśli przepływy gotówkowe są z przeszłości i nie odzwierciedlają bieżącej rzeczywistości, ich wartość może być ograniczona lub nieprzydatna do dalszej analizy.
Funkcja XNPV stanowi potężne narzędzie analizy finansowej w Excelu. Jej zdolność do uwzględniania nieregularnych płatności oraz różnych stop dyskontowych sprawia, że jest niezastąpiona w przypadkach, gdzie standardowe funkcje takie jak NPV nie wystarczają. Dzięki XNPV, analitycy finansowi, inwestorzy oraz specjaliści z różnych dziedzin mogą dokładniej ocenić potencjalne inwestycje oraz podejmować lepsze decyzje.
