Solver w Excelu to ogromnie potężne narzędzie, które od momentu swojego debiutu w lutym 1991 roku pozwala użytkownikom na rozwiązywanie złożonych problemów optymalizacyjnych. Począwszy od prostych równań liniowych, po skomplikowane zadania nieliniowe. Przez ponad trzy dekady Solver ewoluował, stając się nieodzownym dodatkiem, wykorzystywanym w szerokim zakresie aplikacji biznesowych, inżynieryjnych i naukowych. Dzięki niemu możliwe jest znalezienie najlepszego możliwego rozwiązania dla danego zestawu ograniczeń.
Wykorzystanie narzędzia Solver zyskało szczególne znaczenie w sytuacjach wymagających skomplikowanych decyzji optymalizacyjnych. Przykłady takich zastosowań obejmują alokację zasobów w projektach, optymalizację budżetów marketingowych, planowanie produkcji oraz zarządzanie łańcuchem dostaw. Dodatek ten umożliwia zdefiniowanie celu, takiego jak minimalizacja kosztów lub maksymalizacja zysków i następnie automatyczne wyznaczenie najbardziej efektywnego rozwiązania, respektując przy tym wszystkie postawione ograniczenia.
Jako narzędzie, które zdobyło zaufanie milionów użytkowników na całym świecie, Solver w Excelu jest świadectwem tego, jak technologie informatyczne mogą wspierać podejmowanie strategicznych decyzji w biznesie i nie tylko.
Jak włączyć Solver w Excelu?
Solver jest dodatkiem do Excela, który może wymagać aktywacji przed pierwszym użyciem. Aby go włączyć, należy:
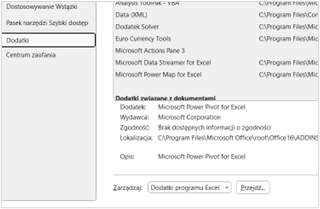
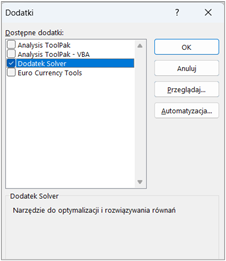
Po wykonaniu tych kroków, Solver będzie dostępny na końcu w zakładce „Dane” na wstążce Excela.

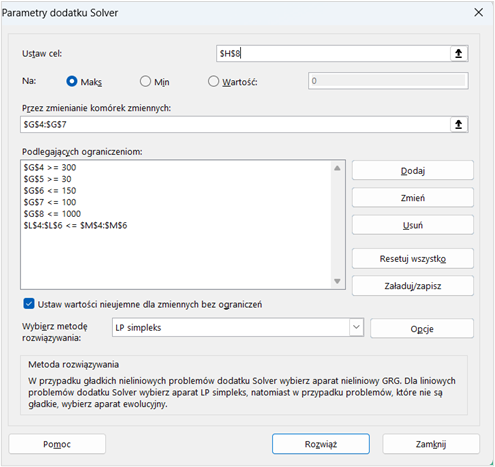
Jak zbudowane jest okno dialogowe narzędzia Solver?
Gdy Solver jest już aktywny, można go uruchomić, klikając „Solver” w zakładce „Dane”. Otworzy się główne okno dialogowe, które jest sercem narzędzia i pozwala na definiowanie problemu optymalizacyjnego:

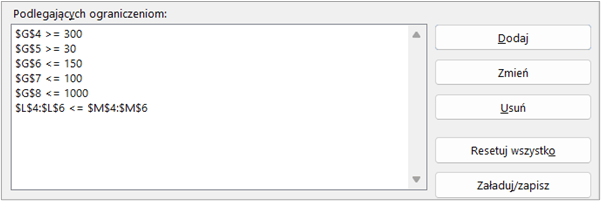
Można również wybrać metodę rozwiązywania, która jest najbardziej odpowiednia dla problemu, oraz dostosować dodatkowe ustawienia w celu zwiększenia skuteczności procesu optymalizacji.
O tym w kolejnym rozdziale…
W Excelu Solver oferuje trzy podstawowe metody rozwiązywania problemów optymalizacyjnych:
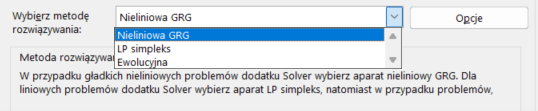
Funkcje nieliniowe są używane do modelowania zależności, w których zmiana jednej zmiennej nie wpływa na inną zmienną w sposób proporcjonalny. Są one wykorzystywane w bardziej skomplikowanych analizach matematycznych, takich jak dynamika systemów, badania naukowe, ekonomia i wiele innych dziedzin, gdzie zależności nie są proste.
Metoda Nieliniowa GRG w Solverze oferuje zaawansowane możliwości dla takich właśnie zadań, umożliwiając skuteczne znajdowanie optymalnych rozwiązań nawet w przypadkach, gdzie tradycyjne metody liniowe zawodzą.
Czym jest opcja Multistart w metodzie nieliniowej?
Opcja Multistart, dostępna w metodzie nieliniowej, jest szczególnie cenna, gdyż pozwala na wielokrotne próby znalezienia globalnego minimum lub maksimum funkcji, co jest kluczowe w sytuacjach, gdy problem ma wiele potencjalnych, tymczasowych najlepszych rozwiązań.
Do czego może służyć opcja „Użyj skalowania automatycznego” w Solverze?
W przypadku modeli które będą zawierać bardzo duże i/lub bardzo małe liczby to dodatek Solver czasem może uznać, że model, który jest liniowy jest nie liniowy. W takim przypadku, żeby tego uniknąć możemy zaznaczyć opcję Użyj skalowania automatycznego w opcjach Solvera i w ten sposób powinien on potraktować model liniowy jako rzeczywiście liniowy.
Opcja „Użyj skalowania automatycznego” może być bardzo przydatna nie tylko w sytuacjach, gdy zachodzi potrzeba uniknięcia błędnej klasyfikacji modeli liniowych jako nieliniowych, ale także szerzej w poprawie stabilności numerycznej i dokładności różnego rodzaju modeli optymalizacyjnych w Solverze.
Przykład funkcji dla metody ewolucyjnej:
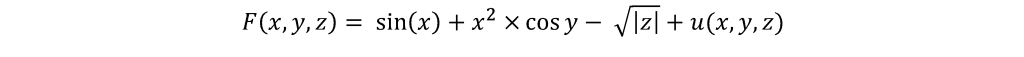
gdzie u(x,y,z) jest funkcją, która może zawierać skoki lub nieregularności, na przykład funkcję modułu lub funkcję składającą się z różnych wyrazów dla różnych zakresów zmiennych.
Dla każdego punktu z tej populacji obliczamy wartość funkcji celu, opierając się na zasadach ewolucji, co pozwala na selekcję i modyfikację punktów w sposób, który zwiększa szanse na znalezienie w przyszłości punktów bliższych tym, które przyniosły lepsze rezultaty. Ponieważ metoda ta opiera się na wartościach funkcji celu zamiast na gradientach funkcji, problemy związane z wieloma lokalnymi ekstremami, a także z funkcjami, dla których nie da się określić gradientu (tzw. funkcje niegładkie), stają się mniej problematyczne.
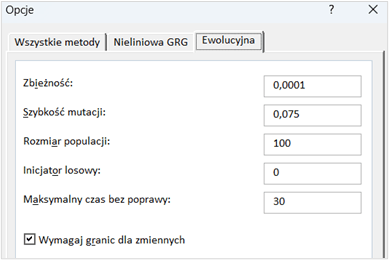
Przy stosowaniu metody ewolucyjnej zaleca się w ustawieniach dostosować szybkość mutacji do poziomu 0,5 i zaznaczyć opcję wymagania ograniczeń dla zmiennych oraz ustawić maksymalny czas bez uzyskania lepszej wartości funkcji celu na 3600 sekund. Dostosowanie szybkości mutacji pomaga uniknąć sytuacji, w której Solver utknie w pobliżu niewłaściwego rozwiązania, a zwiększenie maksymalnego czasu bez poprawy do godziny pozwala na dłuższe poszukiwanie lepszego rozwiązania bez konieczności ciągłej interwencji użytkownika, dając możliwość pozostawienia komputera włączonego do dalszych obliczeń. Więcej na temat mutacji i innych opcji w kolejnym rozdziale.
W tym rozdziale przedstawione zostaną różne opcje konfiguracyjne dostępne w Solverze, począwszy od sposobów precyzji ograniczeń, poprzez skalowanie automatyczne, aż po zaawansowane techniki, takie jak metoda Multistart czy ustawienia specyficzne dla metod ewolucyjnych. Każda z tych opcji dostarcza użytkownikowi narzędzi do dokładniejszego dostosowania procesu rozwiązywania do specyfiki problemu, co jest nieocenione w przypadku bardziej złożonych wyzwań optymalizacyjnych. Zapoznanie się z tymi funkcjami pozwoli lepiej zrozumieć, jak maksymalnie wykorzystać potencjał Solvera, aby osiągnąć najlepsze możliwe wyniki.
Zanim przejdziemy do opcji Solvera warto zapoznać się z kilkoma kluczowymi terminami wykorzystywanymi w optymalizacji.
Czym są problemy Liniowe i Nieliniowe w Solverze?
Załóżmy, że prowadzimy firmę produkującą dwa typy produktów: A i B. Koszt produkcji jednostki produktu A wynosi 5 zł, a produktu B – 10 zł. Mamy ograniczenie budżetowe 100 zł oraz ograniczenie, że możemy wyprodukować maksymalnie 15 sztuk obu produktów łącznie. Naszym celem jest maksymalizacja zysku. Funkcja celu (zysk) i ograniczenia są liniowe względem liczby wyprodukowanych sztuk produktów A i B, co czyni ten problem typowym przykładem optymalizacji liniowej.
Funkcja celu (przykładowa, uproszczona):
Zysk=10x+15y
Ograniczenia:
5x+10y≤100 (ograniczenie budżetowe)
x+y≤15 (ograniczenie ilościowe)
gdzie x i y to liczba sztuk produktów A i B.
Przykład problemu nieliniowego:
Załóżmy, że prowadzona jest optymalizacja składu chemicznego produktu, gdzie nieliniowa reakcja chemiczna między składnikami (x i y) wpływa na jakość produktu. Na przykład, optymalna jakość produktu może być osiągnięta, gdy stosunek składników odpowiada określonemu nieliniowemu związkowi, np. x2+y2=25, co sugeruje, że suma kwadratów proporcji obu składników musi równać się 25, aby uzyskać optymalną jakość. Ponadto, koszt produkcji może wzrastać w sposób nieliniowy w zależności od ilości użytych składników.
Funkcja celu (przykładowa, uproszczona):
Jakość=−(x2+y2−25)2
Ograniczenia: x2+y2=25
gdzie x i y to proporcje składników chemicznych.
Różnica między tymi dwoma przykładami polega na naturze zależności między zmiennymi a funkcją celu oraz ograniczeniami. W pierwszym przykładzie, wszystkie zależności są liniowe, co oznacza, że każda zmiana zmiennej decyzyjnej wpływa na funkcję celu w sposób proporcjonalny. W drugim przykładzie, zależności są nieliniowe, co oznacza, że zmiany zmiennych wpływają na funkcję celu w sposób bardziej złożony, co może prowadzić do pojawienia się wielu lokalnych ekstremów i utrudnia znalezienie optymalnego rozwiązania.
Czym jest problem gładki i niegładki?
W kontekście matematyki i optymalizacji, problem gładki i niegładki odnosi się do natury funkcji celu i ograniczeń w problemie optymalizacyjnym:
Problem gładki:
Optymalizacja funkcji kwadratowej jest klasycznym przykładem gładkiego problemu w optymalizacji. W takim przypadku, funkcja celu jest zazwyczaj przedstawiona jako funkcja kwadratowa, na przykład:
f(x)=ax2+bx+c
gdzie ( a ), ( b ), i ( c ) są stałymi, a ( x ) jest zmienną, którą chcemy zoptymalizować. Ponieważ funkcje kwadratowe są dobrze zrozumiałe i mają łatwe do obliczenia pochodne, proces optymalizacji jest stosunkowo prosty. Pochodna funkcji kwadratowej jest liniowa i wyraża się jako:
f(x)=2ax+b
Problem niegładki:
Problem jest uznawany za niegładki, gdy funkcja celu lub jakiekolwiek ograniczenia nie mają ciągłych pierwszych pochodnych w jednym lub większej liczbie punktów. Może to być spowodowane przez „załamania” lub „kanty” w funkcji celu lub ograniczeniach, co sprawia, że tradycyjne metody optymalizacji oparte na gradientach mogą nie być skuteczne.
Niegładkość funkcji stanowi wyzwanie w optymalizacji, ponieważ brak ciągłych pochodnych utrudnia określenie kierunku, w którym należy się poruszać, aby osiągnąć optimum. W takich przypadkach często stosuje się specjalistyczne techniki, takie jak algorytmy subgradientowe, programowanie proximalne czy metody heurystyczne.
Jaka jest różnica między pochodną a gradientem?
Pochodna opisuje, jak szybko zmienia się wartość funkcji jednej zmiennej w zależności od zmiany tej zmiennej i jest równa nachyleniu stycznej do wykresu funkcji. Gradient jest uogólnieniem pojęcia pochodnej dla funkcji wielu zmiennych i wskazuje kierunek najszybszego wzrostu funkcji w przestrzeni wielowymiarowej, zawierając wszystkie jej cząstkowe pochodne. W kontekście funkcji niegładkich, gdzie tradycyjna pochodna lub gradient nie mogą być zdefiniowane w każdym punkcie, używamy subgradientu, który pozwala na analizę kierunków zmiany wartości funkcji nawet w przypadku jej nieregularności. Subgradienty są kluczowe w algorytmach optymalizacyjnych dla problemów z funkcjami niegładkimi.
Czym jest programowanie proximalne?
Programowanie proximalne to metoda optymalizacji służąca do rozwiązywania problemów, w których funkcja celu może być trudna do zminimalizowania bezpośrednio z powodu jej złożoności lub braku gładkości. Kluczowym elementem tej metody jest dodanie do funkcji celu dodatkowego składnika, zwanego „funkcją proximalną”, która jest zwykle wybrana tak, aby była łatwa do optymalizacji i promowała pewne pożądane właściwości rozwiązania, takie jak rzadkość lub gładkość.
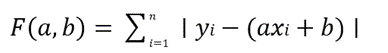
Rozróżnienie między problemami gładkimi a niegładkimi jest kluczowe dla wyboru odpowiedniej metody optymalizacji, ponieważ różne techniki są przystosowane do radzenia sobie z różnymi charakterystykami funkcji celu i ograniczeń.
Do czego służy opcja „ustaw wartości nieujemne dla zmiennych bez ograniczeń”?
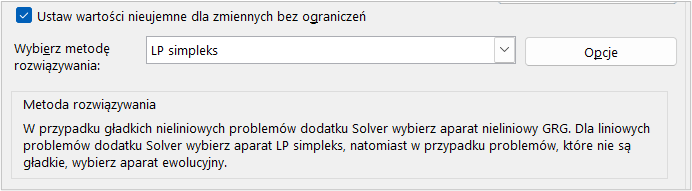
Opcja „Ustaw wartości nieujemne dla zmiennych bez ograniczeń” w głównym oknie Solvera umożliwia automatyczne nałożenie ograniczenia na wszystkie zmienne decyzyjne w modelu, aby przyjmowały one tylko wartości nieujemne (czyli dodatnie lub równe zero). Jest to szczególnie przydatne w problemach optymalizacyjnych, gdzie logiczne lub praktyczne założenia wymagają, aby zmienne nie przyjmowały wartości ujemnych, np. w przypadku ilości produktów, godzin pracy lub innych wielkości, które z natury nie mogą być ujemne.
Zastosowanie tej opcji ma kilka kluczowych zalet:
Co w Solverze oznaczają ograniczenia typu dif, int oraz bin?
W Solverze poza klasycznymi operatorami logicznymi dostępne są również typy ograniczeń „dif”, „int” oraz „bin”:
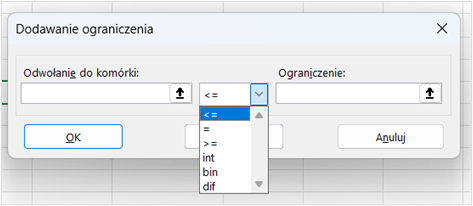
Typy ograniczeń „dif”, „int” i „bin” pozwalają na modelowanie szerokiej gamy problemów optymalizacyjnych, od prostych do bardzo skomplikowanych, dostosowanych do specyficznych potrzeb danego problemu.
Zakładka – Wszystkie Metody
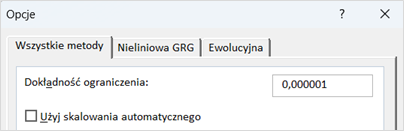
Do czego służy opcja dokładności ograniczenia w Solverze?
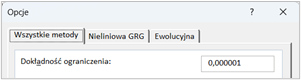
Wyobraźmy sobie, że prowadzona jest mała firma produkcyjna i istnieje potrzeba zminimalizowania kosztów produkcji przy równoczesnym przestrzeganiu pewnych ograniczeń, takich jak maksymalna liczba godzin pracy maszyn (np. 1000 godzin miesięcznie) oraz minimalna ilość produktu, która musi zostać wyprodukowana (np. 500 jednostek miesięcznie). Przy wykorzystaniu Solvera do optymalizacji procesu produkcyjnego, opcja dokładności ograniczenia umożliwia określenie poziomu ścisłości tych limitów. Ustawienie wysokiej dokładności ograniczenia skutkuje dążeniem Solvera do znalezienia rozwiązania, które jak najściślej spełnia te ograniczenia, np. nie przekraczając 1000 godzin pracy maszyn nawet o minutę i produkując dokładnie 500 jednostek produktu lub więcej.
To oznacza, że Solver będzie szukał rozwiązania, które jest bardzo blisko lub dokładnie na granicy określonych warunków, minimalizując przy tym koszty produkcji. Ustawienie dokładności ograniczenia na 0,000001 zapewnia, że Solver będzie szukał rozwiązania, które spełnia te ograniczenia z bardzo wysoką precyzją. Oznacza to, że jeśli Solver znajdzie rozwiązanie, gdzie maszyny pracują 1000,000001 godziny, będzie to traktowane jako naruszenie ograniczeń ze względu na ekstremalnie wysoką dokładność ustawioną w opcjach.
W praktyce taka dokładność zapewnia, że rozwiązania zaproponowane przez Solver są nie tylko optymalne pod względem kosztów, ale także spełniają wymagane ograniczenia z minimalnym możliwym marginesem błędu. W kontekście naszego przykładu, dzięki ustawieniu dokładności na 0,000001, możesz być pewien, że propozycje Solvera dotyczące liczby godzin pracy maszyn i minimalnej produkcji będą jak najbardziej zbliżone do oczekiwanych wartości, co pozwala na skuteczne zarządzanie zasobami i kosztami produkcji.
Czym jest i do czego służy skalowanie automatyczne w Solverze?
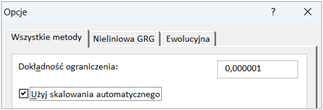
Skalowanie automatyczne w Solverze to funkcja, która ma na celu poprawę stabilności i dokładności rozwiązania problemów optymalizacyjnych, zwłaszcza w przypadkach, gdy problem zawiera zmienne o bardzo różnych wielkościach wartości.
W praktyce, skalowanie automatyczne dostosowuje wielkość danych wejściowych i ograniczeń, aby uniknąć problemów numerycznych, które mogą wystąpić podczas obliczeń. Jest to szczególnie ważne, gdy w modelu występują bardzo duże lub bardzo małe liczby, co może prowadzić do błędów zaokrągleń lub problemów z konwergencją algorytmu Solvera, czyli trudności, które Solver napotyka podczas próby znalezienia najlepszego rozwiązania problemu.
Załóżmy, że w dużym projekcie budowlanym istnieje potrzeba zoptymalizowania alokacji zasobów finansowych (wyrażonych w milionach złotych) oraz czasu pracy maszyn (podanego w godzinach). Bez użycia skalowania automatycznego, znaczna różnica wielkości między wartościami finansowymi a czasowymi może utrudnić Solverowi efektywne odnalezienie optymalnego rozwiązania. Aktywacja skalowania automatycznego umożliwia Solverowi „znormalizowanie” tych wartości, co ułatwia proces optymalizacji i zwiększa prawdopodobieństwo znalezienia najlepszego rozwiązania.
Włączenie tej funkcji jest zalecane w większości przypadków, ponieważ przyczynia się do poprawy ogólnej wydajności Solvera, szczególnie w bardziej złożonych problemach optymalizacyjnych.
W przypadku modeli, które będą zawierać bardzo duże i/lub bardzo małe liczby to dodatek Solver czasem może uznać, że model, który jest liniowy jest nieliniowy. W takim przypadku, żeby tego uniknąć możemy zaznaczyć opcję Użyj skalowania automatycznego w opcjach Solvera i w ten sposób powinien on potraktować model liniowy jako rzeczywiście liniowy.
Chociaż opcja „Użyj skalowania automatycznego” może być bardzo pomocna, nie jest ona domyślnie włączona w Solverze, ponieważ nie w każdej sytuacji jest potrzebna lub pożądana. Niektóre problemy optymalizacyjne są wystarczająco proste i nie wymagają skalowania. Domyślnie wyłączona opcja pozwala uniknąć niepotrzebnego przetwarzania. Excel może zakładać, że dane wejściowe są już odpowiednio przeskalowane lub że użytkownik (ekspert) dostosował dane do swoich potrzeb. Automatyczne skalowanie może w niektórych przypadkach wpłynąć na szybkość rozwiązywania problemu, zwłaszcza w prostszych modelach, gdzie dodatkowe przetwarzanie nie jest wymagane.
Do czego służy opcja pokazywania wyników iteracji w Solverze?
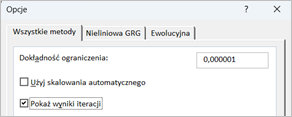
Opcja pokazywania wyników iteracji w Solverze służy do śledzenia postępów Solvera w trakcie poszukiwania optymalnego rozwiązania problemu optymalizacyjnego. Gdy ta opcja jest włączona, Solver wyświetla szczegółowe informacje o każdej iteracji procesu rozwiązywania, w tym wartości zmiennych decyzyjnych, wartość funkcji celu oraz inne statystyki, które mogą być przydatne w ocenie, jak algorytm radzi sobie z danym problemem.
Wyobraźmy sobie, że podejmowane są wysiłki w celu zoptymalizowania logistyki dostaw w danej firmie, z zamiarem minimalizacji kosztów transportu przy jednoczesnym zapewnieniu terminowego dostarczania wszystkich zamówień. Aktywacja opcji pokazywania wyników iteracji umożliwia obserwację zmian proponowanych rozwiązań z każdą iteracją Solvera – jakie trasy zyskują na popularności, w jaki sposób ewoluują koszty oraz jak prędko Solver przybliża się do rozwiązania optymalnego. Pozwala to na głębsze zrozumienie procesu optymalizacji i w razie potrzeby, wprowadzenie korekt w modelu lub ograniczeniach, kierowanych przez wyniki kolejnych iteracji.
Opcja ta jest szczególnie przydatna w przypadku skomplikowanych problemów optymalizacyjnych, gdzie bezpośrednie osiągnięcie rozwiązania jest trudne lub gdy chcemy zrozumieć dynamikę zmian w procesie optymalizacji. To również ułatwia znajdowanie i rozwiązywanie problemów, gdy algorytm ma trudności z osiągnięciem ostatecznego rozwiązania lub w identyfikacji obszarów, w których model może być dalej usprawniony.
Jakie jest zastosowanie opcji ignorowania ograniczeń całkowitoliczbowych w Solverze?
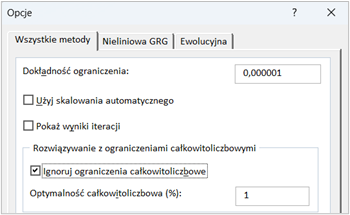
Opcja ignorowania ograniczeń całkowitoliczbowych w Solverze umożliwia tymczasowe wyłączenie wymogu, aby wybrane zmienne decyzyjne przyjmowały wyłącznie wartości całkowite. Jest to przydatne w sytuacjach, gdy chcemy szybko ocenić potencjalne rozwiązania problemu bez narzucania na nie sztywnych ograniczeń całkowitoliczbowych, co może ułatwić znalezienie ogólnego kierunku, w jakim należy podążać w poszukiwaniach optymalnego rozwiązania.
Załóżmy, że produkcja jest planowana w danej firmie, gdzie konieczna jest decyzja o liczbie jednostek każdego produktu do wyprodukowania. Celem jest maksymalizacja zysku w ramach określonych ograniczeń produkcyjnych. Wiele ze zmiennych decyzyjnych naturalnie przyjmuje wartości całkowite (np. produkcja pół produktu nie jest możliwa). Jednakże, w początkowej fazie planowania, rozważane może być zignorowanie ograniczeń całkowitoliczbowych w celu szybszego zidentyfikowania optymalnych proporcji produkcji między różnymi produktami, bez obaw o konieczność zaokrąglania wyników do całkowitych jednostek.
Takie podejście może pomóc w szybszym zidentyfikowaniu ogólnej strategii optymalizacji, która następnie może zostać dostosowana i uszczegółowiona, włączając ponownie ograniczenia całkowitoliczbowe, aby doprecyzować końcowe rozwiązanie zgodne z realnymi wymogami produkcji.
Czym jest optymalność całkowitoliczbowa w kontekście Solvera?

Optymalność całkowitoliczbowa w kontekście Solvera odnosi się do sposobu, w jaki Solver dąży do znalezienia najlepszego możliwego rozwiązania problemu optymalizacyjnego, które spełnia wszystkie narzucone ograniczenia, w tym wymóg, aby pewne zmienne decyzyjne przyjmowały wartości całkowite. W wielu problemach optymalizacyjnych, zwłaszcza tych dotyczących planowania, alokacji zasobów czy harmonogramowania, istotne jest, by rozwiązania były nie tylko optymalne z punktu widzenia funkcji celu, ale również, aby były „całkowite” – na przykład, nie można zatrudnić pół pracownika lub wyprodukować pół produktu.
Optymalność całkowitoliczbowa gwarantuje, że otrzymane rozwiązanie nie tylko jest optymalne z matematycznego punktu widzenia, ale również praktyczne i realne do zastosowania w rzeczywistych warunkach. Solver wykorzystuje różne techniki matematyczne i algorytmy, aby zbliżyć się do optymalnego rozwiązania, które spełnia wszystkie ograniczenia, w tym całkowitoliczbowość, jednocześnie minimalizując lub maksymalizując określoną funkcję celu.
W praktyce, osiągnięcie optymalności całkowitoliczbowej może wymagać od Solvera dodatkowych obliczeń i zastosowania specjalnych metod, takich jak metoda gałęzi i granic( (ang. Branch and Bound, B&B) to algorytm optymalizacyjny wykorzystywany w Solverze do rozwiązywania problemów optymalizacji dyskretnej, czyli takich, gdzie zmienne decyzyjne muszą przyjmować wartości całkowite, często spotykany w problemach programowania całkowitoliczbowego. ), która pozwala na efektywne przeszukiwanie przestrzeni rozwiązań w poszukiwaniu najlepszego rozwiązania spełniającego wszystkie warunki, w tym całkowitoliczbowość zmiennych decyzyjnych.
Jeśli opcja optymalności całkowitoliczbowej jest ustawiona na 1%, oznacza to, że Solver uzna rozwiązanie za wystarczająco dobre, jeśli będzie ono w zakresie 1% od optymalnego rozwiązania teoretycznego. Na przykład, jeśli najlepsze teoretyczne rozwiązanie problemu optymalizacyjnego ma wartość funkcji celu równą 100, to Solver zaakceptuje jako rozwiązanie każde, którego wartość funkcji celu znajduje się w zakresie 99 do 101.
To ustawienie jest szczególnie przydatne w przypadkach, gdy poszukiwanie absolutnie najlepszego rozwiązania (z dokładnością do najmniejszej możliwej jednostki) byłoby zbyt czasochłonne lub skomplikowane z powodu złożoności problemu. Pozwala to na znalezienie praktycznego rozwiązania w rozsądnym czasie, z akceptowalnym poziomem przybliżenia do idealnego wyniku.
Do czego służy ustawienie maksymalnego czasu pracy Solvera?

Ustawienie maksymalnego czasu pracy Solvera pozwala określić maksymalny czas, przez który Solver będzie próbował znaleźć rozwiązanie problemu optymalizacyjnego. Jest to przydatna funkcja, która pomaga kontrolować czas trwania procesu optymalizacji, szczególnie w przypadkach, gdy rozwiązanie problemu może być czasochłonne ze względu na jego złożoność lub gdy istnieje ryzyko, że Solver wpadnie w pętlę nieskończoną.
Zastosowanie tego ustawienia pozwala użytkownikowi na zaplanowanie, jak długo Solver będzie pracował nad danym problemem, zanim automatycznie zatrzyma proces rozwiązywania. Jest to szczególnie ważne w środowiskach biznesowych lub naukowych, gdzie czas jest cennym zasobem, i nie można pozwolić sobie na nieograniczone czasowo procesy obliczeniowe.
Załóżmy, że jest prowadzona praca nad optymalizacją rozmieszczenia produktów w magazynie, aby zminimalizować czas potrzebny na kompletację zamówień. Problem ten jest jednak złożony i obejmuje wiele zmiennych oraz ograniczeń. Ustawienie maksymalnego czasu pracy Solvera, na przykład na 30 minut, ograniczy czas poszukiwań optymalnego rozwiązania. Jeżeli w tym czasie Solver znajdzie najlepsze możliwe rozwiązanie, będzie to doskonały wynik. W przeciwnym razie, proces zostanie zatrzymany po upływie określonego czasu, co umożliwi ocenę dotychczas znalezionych rozwiązań lub zmianę strategii rozwiązywania problemu.
Czym jest liczba iteracji w Solverze?
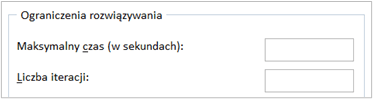
Limit liczby iteracji w Solverze określa maksymalną liczbę prób, które Solver podejmie, aby znaleźć rozwiązanie problemu optymalizacyjnego. Jest to ważne ustawienie, które pozwala kontrolować proces rozwiązywania, szczególnie w sytuacjach, gdy poszukiwanie optymalnego rozwiązania może być złożone i czasochłonne.
Znaczenie limitu liczby iteracji:
Załóżmy, że jest prowadzona praca nad optymalizacją trasy dostaw dla floty pojazdów dystrybucyjnych. Problem ten jest skomplikowany, ponieważ należy wziąć pod uwagę wiele czynników, takich jak czas dostawy, koszty paliwa i ograniczenia czasu pracy kierowców. Ustawienie limitu liczby iteracji na 1000 umożliwia Solverowi wykonanie maksymalnie 1000 prób znalezienia najbardziej efektywnej trasy przed zatrzymaniem procesu. Dzięki temu można znaleźć rozwiązanie w rozsądnym czasie, nawet jeśli nie będzie to najlepsze możliwe rozwiązanie, zapewniając przy tym, że zasoby obliczeniowe nie będą nadmiernie eksploatowane.
Czym są ograniczenia ewolucyjne i całkowitoliczbowe?

Ograniczenia ewolucyjne i całkowitoliczbowe w Solverze odnoszą się do specyficznych typów ograniczeń, które mogą być stosowane w problemach optymalizacyjnych rozwiązywanych za pomocą metody ewolucyjnej. Ograniczenia całkowitoliczbowe wymagają, aby wybrane zmienne decyzyjne przyjmowały jedynie wartości całkowite, natomiast ograniczenia ewolucyjne są związane z metodą ewolucyjną, która jest stosowana do rozwiązywania problemów, gdzie tradycyjne metody (takie jak liniowa czy nieliniowa optymalizacja) mogą nie być efektywne. Metoda ewolucyjna wykorzystuje techniki inspirowane procesami ewolucji biologicznej, takie jak selekcja, krzyżowanie i mutacja, do eksploracji przestrzeni rozwiązań w poszukiwaniu optymalnego rozwiązania problemu.
Czym jest Maksymalna liczba podproblemów w Solverze?

Maksymalna liczba podproblemów w Solverze określa limit liczby podproblemów, które Solver może wygenerować i zbadać podczas poszukiwania rozwiązania problemu optymalizacyjnego, szczególnie w kontekście metody ewolucyjnej. Jest to parametr kontrolujący głębokość i zakres eksploracji przestrzeni rozwiązań przez algorytm, ograniczając liczbę różnych ścieżek poszukiwań, które algorytm może równocześnie śledzić. Ustawienie tego limitu pomaga w zarządzaniu złożonością obliczeniową procesu rozwiązywania, a także w optymalizacji czasu potrzebnego na znalezienie rozwiązania, balansując między dokładnością a wydajnością obliczeniową.
Przykładowo wyobraź sobie, że masz duży karton klocków LEGO i chcesz zbudować z nich wiele różnych modeli samochodów. Każdy model samochodu to „podproblem”, czyli mały projekt, który możesz zrealizować, używając klocków. Solver stara się znaleźć najlepsze rozwiązanie matematycznego problemu.
Mówiąc o „maksymalnej liczbie podproblemów” w Solverze, to jakbyś miał limit, ile różnych modeli samochodów możesz zacząć budować jednocześnie. Jeśli masz limit równy 10, to oznacza, że możesz pracować nad budowaniem jednocześnie tylko 10 modeli samochodów. Jeśli chcesz spróbować zbudować więcej modeli, musisz najpierw skończyć pracę nad jednym z tych, nad którymi już pracujesz, zanim zaczniesz nowy.
W przypadku Solvera, jeśli ustawisz maksymalną liczbę podproblemów na 10, oznacza to, że algorytm będzie próbował znaleźć najlepsze rozwiązanie, eksplorując jednocześnie maksymalnie 10 różnych ścieżek lub opcji. To pomaga komputerowi skoncentrować się na najbardziej obiecujących opcjach, zamiast próbować wszystkiego naraz, co mogłoby zająć bardzo dużo czasu.
Czym jest maksymalna liczba dopuszczalnych rozwiązań?

W Solverze, ustawiając maksymalną liczbę dopuszczalnych rozwiązań, decydujesz, ile różnych rozwiązań problemu algorytm może rozważyć jako „dobre” lub wystarczająco bliskie idealnemu rozwiązaniu, zanim zatrzyma poszukiwania. To pomaga skupić się na najbardziej obiecujących rozwiązaniach, ograniczając jednocześnie ilość czasu i zasobów komputera potrzebnych na znalezienie najlepszego rozwiązania.
Zakładka – Nieliniowa GRG
Do czego służy opcja zbieżności w metodzie nieliniowej GRG Solvera?
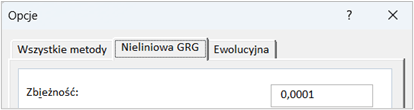
Opcja zbieżności w metodzie nieliniowej GRG (Generalized Reduced Gradient) w Solverze służy do określenia, jak blisko rozwiązania muszą być kolejne iteracje algorytmu, aby uznać, że proces optymalizacji osiągnął punkt zbieżności, czyli moment, w którym dalsze iteracje nie przynoszą już znaczącej poprawy rozwiązania. W praktyce jest to wartość progowa, która określa minimalną różnicę między wynikami dwóch kolejnych iteracji, przy której algorytm może zatrzymać poszukiwania, uznając, że znalazł optymalne (lub wystarczająco dobre) rozwiązanie.
Załóżmy, że jest prowadzona praca nad optymalizacją formuły składu chemicznego produktu w celu zwiększenia jego wydajności, biorąc pod uwagę różnorodne składniki i ich proporcje. Wykorzystanie metody nieliniowej GRG oraz odpowiednie ustawienie opcji zbieżności umożliwi znalezienie optymalnej kombinacji składników, jednocześnie zapewniając, że proces poszukiwań zostanie zakończony w rozsądnym czasie. Taki proces pozwoli osiągnąć rozwiązanie, które spełnia zadane kryteria wydajności z akceptowalną dokładnością.
Jakie jest znaczenie obliczania pochodnych 'w przód’ i 'centralnie’ w Solverze?
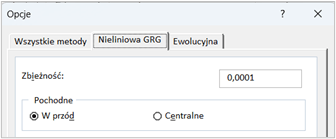
Obliczanie pochodnych w przód i centralnie w Solverze jest metodą, dzięki której program może lepiej zrozumieć, jak małe zmiany w wartościach zmiennych decyzyjnych wpływają na wynik funkcji celu, czyli na to, co próbujemy zoptymalizować. To trochę jak próbowanie zrozumieć, jak zmienia się prędkość samochodu, gdy delikatnie dociskasz lub puszczasz pedał gazu.
Obliczanie pochodnych 'w przód’ polega na tym, że Solver patrzy, co się stanie z wartością funkcji celu, gdy zwiększymy wartość zmiennej decyzyjnej o małą, stałą ilość. To jak zobaczyć, jak zmienia się prędkość samochodu, gdy naciskasz pedał gazu.
Obliczanie pochodnych 'centralnie’ jest bardziej zaawansowaną techniką, gdzie Solver sprawdza, co się dzieje z funkcją celu, gdy zmieniamy wartość zmiennej decyzyjnej zarówno w górę, jak i w dół o małą ilość. Jest to bardziej dokładny sposób na zrozumienie, jak funkcja celu reaguje na zmiany, ponieważ bierze pod uwagę zmiany z obu stron. To jak sprawdzenie, jak zmienia się prędkość samochodu, gdy delikatnie dociskasz lub puszczasz pedał gazu, i porównanie obu reakcji.
Obliczanie pochodnych w obu tych sposobach pomaga Solverowi lepiej nawigować w procesie optymalizacji, co jest szczególnie ważne w problemach nieliniowych, gdzie relacje między zmiennymi a funkcją celu mogą być skomplikowane. Ułatwia to znalezienie kierunku, w którym należy się poruszać, aby znaleźć najlepsze możliwe rozwiązanie problemu.
Załóżmy, że firma produkująca stoły dąży do zminimalizowania kosztów produkcji przy jednoczesnym zachowaniu jakości. Celem jest określenie optymalnej liczby godzin pracy maszyn (x) i ilości materiału (y), mających wpływ na całkowity koszt (C).
Jeśli masz funkcję kosztu:
C(x,y)=100x+50y
W praktyce, jeśli obliczenia pokażą, że zwiększenie godzin pracy maszyn (x) o jedną godzinę zwiększa koszt o więcej niż oszczędności z tytułu mniejszego zużycia materiału (y), to strategią minimalizacji kosztów będzie redukcja godzin pracy. Pochodne pozwalają na takie analizy, dostarczając informacji, które kierunki zmian są najbardziej obiecujące dla osiągnięcia celu optymalizacji.
Czym jest i do czego służy opcja Multistartu w Solverze?

Opcja Multistartu w Solverze jest techniką stosowaną głównie w metodach optymalizacji nieliniowej, która pozwala na poszukiwanie globalnego optimum problemu poprzez wielokrotne rozpoczynanie procesu optymalizacji z różnych, losowo wybranych punktów startowych. Celem tej metody jest zwiększenie szansy na znalezienie najlepszego możliwego rozwiązania, unikając pułapek lokalnych minimów lub maksimów, które mogą nie być optymalnym rozwiązaniem całego problemu.
Metoda ta jest szczególnie przydatna w problemach, gdzie zależności między zmiennymi są nieliniowe oraz w sytuacjach, gdy problem zawiera wiele zmiennych decyzyjnych, co sprawia, że tradycyjne metody mogą mieć trudności z efektywnym znalezieniem globalnego optimum.
Załóżmy, że jest prowadzona firma produkująca specjalistyczne urządzenia, gdzie cel stanowi optymalizacja projektu pod względem kosztu produkcji i efektywności energetycznej. Problem ten charakteryzuje się złożonością, wymagając zbalansowania różnorodnych czynników, takich jak wybór materiałów, konstrukcja i procesy produkcyjne, które są ze sobą silnie powiązane w sposób nieliniowy.
Stosując opcję Multistartu, Solver może rozpocząć poszukiwanie optymalnego projektu z wielu różnych „punktów startowych”, co pozwala na eksplorację różnych kombinacji czynników. Dzięki temu masz większą szansę na znalezienie projektu, który oferuje najlepszy kompromis między kosztem a efektywnością, unikając rozwiązań, które są optymalne tylko lokalnie, ale nie globalnie.
Czym jest rozmiar populacji w metodzie Multistartu?
Rozmiar populacji w metodzie Multistartu w Solverze ma kluczowe znaczenie dla procesu rozwiązywania problemów optymalizacyjnych, szczególnie tych o charakterze nieliniowym. Populacja w tym kontekście oznacza zbiór różnych punktów startowych, z których algorytm rozpoczyna poszukiwanie optymalnego rozwiązania.
Wpływ rozmiaru populacji:
Załóżmy, że jest prowadzona praca nad optymalizacją mieszanki składników dla nowego produktu spożywczego. Celem jest osiągnięcie produktu, który jest zarówno smaczny, jak i odżywczy, z dostępnością różnych składników o zróżnicowanych właściwościach smakowych i odżywczych. Przy wykorzystaniu w Solverze metody Multistart z dużą populacją punktów startowych, możliwe jest przetestowanie wielu różnych kombinacji składników, co zwiększa szanse na znalezienie optymalnej mieszanki. Jednakże, należy być przygotowanym na to, że taki proces może wymagać więcej czasu, niż w przypadku wyboru mniejszej liczby punktów startowych.
Do czego służy inicjator losowy w opcjach Multistartu i ewolucyjnej Solvera?

Inicjator losowy w opcjach Multistartu i metody nieliniowej GRG Solvera służy do określenia początkowego punktu (lub punktów) dla algorytmu poszukiwania rozwiązania, wprowadzając element losowości do procesu wyboru punktów startowych. W metodzie Multistartu, gdzie proces optymalizacji jest uruchamiany wielokrotnie z różnych punktów startowych, inicjator losowy decyduje o tym, jak te punkty startowe są rozłożone w przestrzeni rozwiązań.
Zastosowanie inicjatora losowego:
„Inicjator losowy” (ang. random seed) to wartość używana do inicjowania generatora liczb losowych w algorytmach, które wykorzystują losowość, np. przy wybieraniu punktów startowych w opcji Multistart. Jeśli to pole jest puste, oznacza to, że każde uruchomienie Solvera może użyć innego zestawu liczb losowych, co prowadzi do generowania różnych punktów startowych przy każdym uruchomieniu. Inicjator losowy domyślnie jest pusty.
Ustawienie inicjatora losowego na konkretną wartość, np. 1 lub 50, sprawia, że proces generowania punktów startowych jest powtarzalny:
Podsumowując, puste pole inicjatora losowego daje różne punkty startowe przy każdym uruchomieniu, co zwiększa eksplorację przestrzeni rozwiązań, natomiast ustawienie konkretnego inicjatora losowego zapewnia powtarzalność punktów startowych, co ułatwia analizę i porównywanie wyników.
Załóżmy, że jest optymalizowany plan treningowy dla sportowca, z celem znalezienia najlepszego balansu między treningiem siłowym a cardio, aby maksymalizować ogólną wydajność. Przy zastosowaniu metody nieliniowej GRG z inicjatorem losowym, proces optymalizacji może być rozpoczęty od wielu różnych „planów treningowych”, co zwiększa szanse na znalezienie najbardziej efektywnego planu, prowadzącego do optymalnych wyników sportowych. Ustawienie konkretnego ziarna losowego umożliwi powtórzenie eksperymentu i potwierdzenie wyników.
Czym jest i do czego służy wymaganie granic dla zmiennych w Solverze?
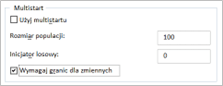
Opcja „Wymagaj granic dla zmiennych” w formie checkboxa w Solverze służy do wskazania, czy Solver powinien uwzględniać określone granice dla zmiennych decyzyjnych podczas procesu optymalizacji. Zaznaczenie tej opcji informuje Solver, że wszystkie zmienne decyzyjne będą miały określone ograniczenia. Jednak samo zaznaczenie tej opcji nie ustala wartości tych granic – to użytkownik musi zrobić osobno.
Granice dla zmiennych ustala się w sekcji „Ograniczenia” w oknie dialogowym Solvera.
Każda zmienna decyzyjna może mieć określone różne ograniczenia, a ich wartości są ustalane indywidualnie przez użytkownika w oparciu o potrzeby i specyfikę danego problemu optymalizacyjnego. Warto pamiętać, że ustawienie realistycznych i adekwatnych do problemu granic jest kluczowe dla skuteczności i efektywności procesu optymalizacji.
Chociaż określenie granic dla wszystkich zmiennych nie jest absolutnie wymagane (można odznaczyć opcję „Wymagaj granic dla zmiennych”), jest to praktycznie niezbędne, aby Solver mógł znaleźć dobre rozwiązania w rozsądnym czasie.
Zakładka – Ewolucyjna
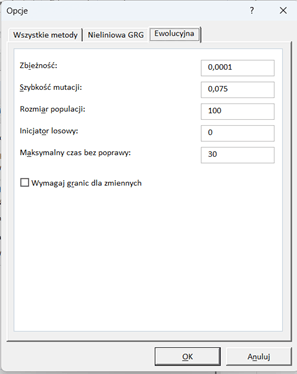
Do czego służy opcja zbieżności w metodzie ewolucyjnej Solvera?
Opcja zbieżności w metodzie ewolucyjnej Solvera służy do określenia, kiedy algorytm może przestać szukać lepszego rozwiązania, ponieważ uzna, że znalezione dotychczas jest wystarczająco dobre. Można to porównać do gry w ciepło-zimno, gdzie zbliżasz się do ukrytego przedmiotu: im bliżej celu, tym „cieplej”. Opcja zbieżności mówi Solverowi, jak „ciepło” musi być, żeby uznać, że jesteś wystarczająco blisko szukanego przedmiotu, czyli optymalnego rozwiązania.
W praktyce, poprzez ustawienie opcji zbieżności, definiuje się, jak niewielka różnica między kolejnymi rozwiązaniami (iteracjami algorytmu) jest akceptowalna, aby uznać, że dalsze poszukiwania nie przyniosą już znaczącej poprawy. Na przykład, ustalenie zbieżności na niską wartość informuje Solver, że oczekiwane jest bardzo dokładne dopasowanie do optymalnego rozwiązania przed zakończeniem poszukiwań.
Z kolei, wybór wyższej wartości zbieżności sygnalizuje, że mniejsze ulepszenia rozwiązania między iteracjami nie są istotne i Solver może zakończyć pracę szybciej, akceptując rozwiązanie, które jest „blisko” optymalnego, ale niekoniecznie jest absolutnie najlepsze.
Czym jest i do czego służy szybkość mutacji w metodzie ewolucyjnej w Solverze?

Szybkość mutacji w metodzie ewolucyjnej Solvera odnosi się do częstotliwości, z jaką algorytm wprowadza losowe zmiany (mutacje) w zmiennych decyzyjnych podczas procesu poszukiwania optymalnego rozwiązania. Jest to kluczowy parametr w algorytmach ewolucyjnych, który ma na celu zapewnienie różnorodności genetycznej w populacji rozwiązań, co pomaga w eksploracji przestrzeni rozwiązań i zapobiega utknięciu algorytmu w lokalnych minimach lub maksimach.
Do czego to służy:
Szybkość mutacji jest większa przy wartości 2, co sprzyja szerokiej eksploracji, podczas gdy wartość 0,1 prowadzi do bardziej konserwatywnej, lokalnej eksploracji. Wybór odpowiedniej wartości zależy od konkretnego problemu i tego, czy bardziej potrzebujemy eksploracji czy eksploatacji w procesie poszukiwania optymalnego rozwiązania.
Załóżmy, że jest prowadzona optymalizacja schematu treningowego dla grupy sportowców, gdzie poszukiwane jest idealne połączenie różnych typów aktywności fizycznej (siłowej, wytrzymałościowej, szybkościowej) odpowiadające ich indywidualnym potrzebom. Ustawienie wyższej szybkości mutacji pozwala na częstsze eksperymentowanie z różnymi kombinacjami treningowymi, co zwiększa szansę na znalezienie najbardziej efektywnego schematu dla każdego sportowca. Jednak, jeśli zaobserwowane zostanie, że algorytm zbyt często oddala się od już dobrych rozwiązań, może zostać rozważone obniżenie szybkości mutacji, co umożliwi skupienie się na dokładniejszej optymalizacji wokół obiecujących rozwiązań.
Jak rozmiar populacji wpływa na algorytm ewolucyjny w Solverze?

Rozmiar populacji w algorytmie ewolucyjnym w Solverze ma istotny wpływ na proces poszukiwania optymalnego rozwiązania problemu optymalizacyjnego. Populacja w tym kontekście oznacza zbiór potencjalnych rozwiązań (kandydatów), z których każde jest ewaluowane w celu znalezienia najlepszego rozwiązania.
Wpływ rozmiaru populacji:
Wybór odpowiedniego rozmiaru populacji jest kwestią balansu między potrzebą eksploracji przestrzeni rozwiązań a ograniczeniami zasobów obliczeniowych i czasu. W niektórych przypadkach, mniejsza populacja może być bardziej efektywna, szczególnie jeśli problem jest mniej złożony, natomiast w przypadku bardziej złożonych problemów, większa populacja może przynieść lepsze wyniki kosztem większych wymagań obliczeniowych.
Do czego służy opcja maksymalnego czasu bez poprawy w metodzie ewolucyjnej w Solverze?

Opcja maksymalnego czasu bez poprawy w metodzie ewolucyjnej Solvera jest mechanizmem, który pozwala na zakończenie procesu optymalizacji, jeśli przez określony czas wyrażony w sekundach nie zostaną znalezione lepsze rozwiązania. Oznacza to, że algorytm przestanie szukać nowych, potencjalnie lepszych kandydatów na rozwiązanie, jeżeli przez ustalony okres nie dojdzie do poprawy wartości funkcji celu.
Do czego to służy:
Załóżmy, że jest prowadzona optymalizacja rozmieszczenia produktów w magazynie, mająca na celu minimalizację czasu potrzebnego na kompletowanie zamówień. Wykorzystanie metody ewolucyjnej umożliwia eksplorację różnych konfiguracji rozmieszczenia. Ustawienie opcji maksymalnego czasu bez poprawy na 10 minut (600 sekund) pozwala na zakończenie procesu optymalizacji, jeżeli przez ten czas nie zostanie znalezione lepsze rozmieszczenie niż dotychczas najlepsze. Dzięki temu, nawet bez odnalezienia idealnego rozmieszczenia, jest uzyskiwane najlepsze dostępne rozwiązanie w rozsądnym czasie, co pozwala na uniknięcie nadmiernego wydłużania procesu optymalizacji.
Przykład 1
W tym przykładzie nieliniowym chcemy zobaczyć wysokość raty, która nie będzie przekraczała 3500zł dla kredytu co najmniej 100 000zł przy rocznej stopie procentowej 5,6%. Do znalezienia tej raty musimy posłużyć się funkcją finansową PMT, o której więcej można się dowiedzieć w tym miejscu – blog PMT.

Przykład 2
Chcemy znaleźć optymalny sposób na dystrybucję naszych produktów, tak aby zminimalizować całkowity koszt transportu, jednocześnie spełniając wszystkie wymagania klientów i nie przekraczając możliwości produkcyjnych naszych fabryk. Musimy określić, jakie ilości i z których lokalizacji powinniśmy wysyłać, aby nasze działania były kosztowo efektywne, a jednocześnie nie naruszały umów z klientami oraz możliwości produkcyjnych. Solver pomoże nam ustalić, jak rozdzielić produkcję między fabryki i jak zorganizować logistykę, aby koszty transportu były jak najniższe, z zachowaniem wysokiej jakości i terminowości dostaw.
Przykład 3
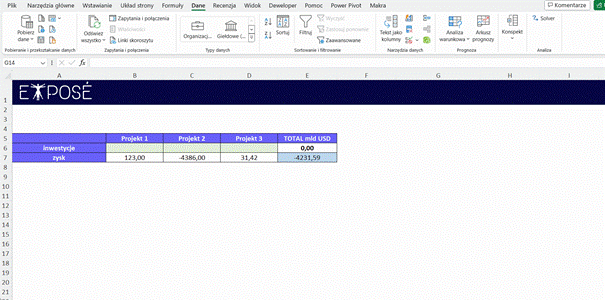
Chcemy znaleźć optymalną alokację budżetu w wysokości 100 milionów USD na trzy różne projekty inwestycyjne. Naszym celem jest maksymalizacja potencjalnego zwrotu z inwestycji, jednocześnie unikając ryzyka strat, które mogłyby przekroczyć wartość zainwestowanych środków. Każdy z projektów może być sfinansowany w różnej kwocie, a oczekiwane zyski lub straty zostały oszacowane i przedstawione w odpowiednim wierszu arkusza kalkulacyjnego. Musimy określić, w jaki sposób podzielić dostępny budżet między te projekty, aby zwiększyć prawdopodobieństwo osiągnięcia maksymalnych zysków przy założonych ograniczeniach.
Zadanie to jest skomplikowane przez nieliniowy charakter zysków, które są przewidywane dla każdego z projektów B7, C7 i D7.
Podczas naszej szczegółowej analizy i praktycznych przykładów z wykorzystaniem narzędzia Solver w Excelu, zgłębiliśmy zarówno jego podstawowe funkcje, jak i zaawansowane opcje optymalizacyjne. Poznaliśmy metody włączania Solvera oraz strukturę jego interfejsu użytkownika. Rozważaliśmy różnice między problemami liniowymi i nieliniowymi, gładkimi oraz niegładkimi, a także nauczyliśmy się interpretować pochodne i gradienty. Zajęliśmy się również takimi koncepcjami, jak programowanie proximalne i użycie skalowania automatycznego dla poprawy dokładności obliczeń.
Wyeksplorowaliśmy szczególnie istotne w praktyce kwestie, takie jak ustawianie wartości nieujemnych dla zmiennych, rozumienie ograniczeń typu dif, int oraz bin, i zastosowanie opcji dokładności ograniczenia dla bardziej precyzyjnej optymalizacji. Przeanalizowaliśmy wykorzystanie metody Multistart oraz wpływ szybkości mutacji i rozmiaru populacji w metodzie ewolucyjnej, co pomogło nam zrozumieć, jak Solver radzi sobie z kompleksowymi problemami, które wymagają globalnego podejścia do poszukiwania optymalnych rozwiązań.
Solver okazał się być narzędziem niezwykle potężnym, zdolnym do rozwiązywania zarówno skomplikowanych zadań biznesowych, jak i prostszych, codziennych problemów finansowych. Demonstracja jego zdolności w praktycznych zastosowaniach, takich jak planowanie budżetu czy optymalizacja planów treningowych, pokazała jego wszechstronność i dostępność dla użytkowników na różnych poziomach zaawansowania.
W konkluzji, Solver w Excelu jest narzędziem nieocenionym dla tych, którzy pragną podejmować decyzje oparte na solidnych analizach optymalizacyjnych, oferując elastyczność i głębię w rozwiązywaniu szerokiej gamy problemów optymalizacyjnych.
